Calculus: Integration
Contents (6 topics • 33 videos)
Documents
Basic Integration Formulas (.PDF) 
Properties of Definite Integrals
Theorems and Definitions
Properties of Definite Integrals
If \(f\) is defined at \(x=a\), then
\[ \int_{a}^{a}{ f(x) \text{ } dx } = 0. \]
If \(f\) is integrable on \([a, b]\), then
\[ \int_{b}^{a}{ f(x) \text{ } dx } = - \int_{a}^{b}{ f(x) \text{ } dx }. \]
If \(f\) is integrable on the three closed intervals determined by \(a\), \(b\), and \(c\), then
\[ \int_{a}^{b}{ f(x) } \text{ } dx = \int_{a}^{c}{ f(x) } \text{ } dx + \int_{c}^{b}{ f(x) } \text{ } dx. \]
If \(f\) and \(g\) are integrable on \([a, b]\) and \(k\) is a constant, then the functions \(kf\) and \(f \pm g\) are integrable on \([a, b]\), and
\[ \int_{a}^{b}{ k \cdot f(x) } \text{ } dx = k \int_{a}^{b}{ f(x) } \text{ } dx \]
\[ \int_{a}^{b}{ \Big[ f(x) \pm g(x) \Big] } \text{ } dx = \int_{a}^{b}{ f(x) } \text{ } dx \pm \int_{a}^{b}{ g(x) } \text{ } dx \]
Evaluate each definite integral using geometric formulas.
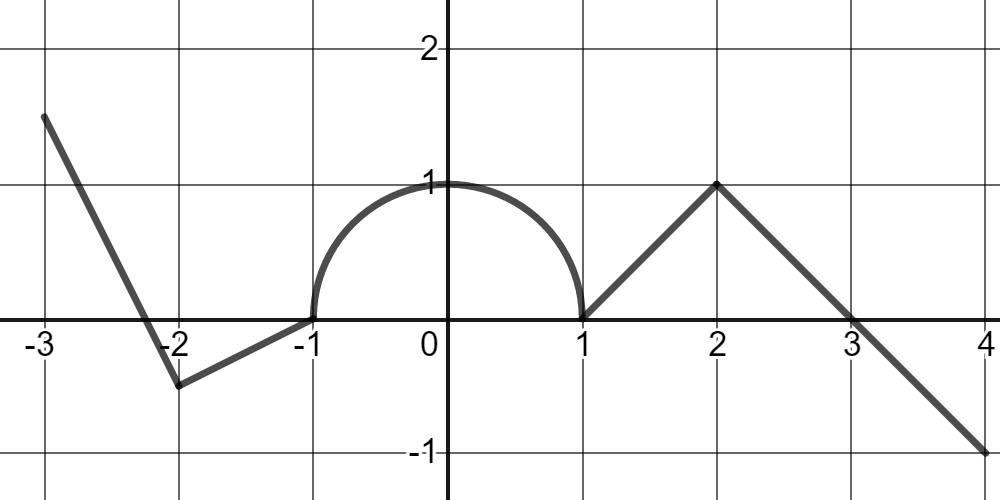
Using Properties of Definite Integrals
\[ \int_{0}^{2}{ f(x) } \text{ } dx = 3 \quad \int_{2}^{6}{ f(x) } \text{ } dx = -2 \]
Integration Using a Change of Variables (U-Substitution)
Theorems and Definitions
Change of Variables for Indefinite Integrals
Let \(g\) be a function whose range is an interval \(I\), and let \(f\) be a function that is continuous on \(I\). If \(g\) is differentiable on its domain and \(F\) is an antiderivative of \(f\) on \(I\), then
\[ \int{ f \big( g(x) \big) \cdot g'(x) } \text{ } dx = F \big( g(x) \big) + C. \]
Letting \(u=g(x)\) gives \(du=g'(x) \text{ } dx \) and
\[ \int{ f(u) } \text{ } du = F(u) + C. \]
Change of Variables for Definite Integrals
If the function \(u=g(x)\) has a continuous derivative on the closed interval \([a, b]\) and \(f\) is continuous on the range of \(g\), then
\[ \int_{a}^{b}{ f \big( g(x) \big) \cdot g'(x) } \text{ } dx = \int_{g(a)}^{g(b)}{ f(u) } \text{ } du. \]
Integrate.
\[ \int{ \sqrt{6-\sqrt{x-2}} } \text{ } dx \]
Integrate.
\[ \int{ \frac{2x}{(x-2)^2} } \text{ } dx \]
Integrate.
\[ \int{ \frac{(\ln{x}+2)^4(4-\ln{x})}{6x} } \text{ } dx \]
Integrate.
\[ \int{ \frac{12}{x \ln{x^4}} } \text{ } dx \]
Integrate.
\[ \int{ \frac{4 + \sqrt{x}}{4 - \sqrt{x} }} \text{ } dx \]
Integrate.
\[ \int{ \frac{x}{(x+1)-\sqrt{x+1}} } \text{ } dx \]
Integrate.
\[ \int{ \frac{2}{\sqrt{x}(x+4)} } \text{ } dx \]
Integrate in two ways.
\[ \int{ 2 \tan{x} \cdot \sec ^2{x} } \text{ } dx \]
Integrate.
\[ \int{ \frac{1}{\sqrt{x}(4-2\sqrt{x})} } \text{ } dx \]
Evaluate.
\[ \int_{1}^{e}{ \frac{(\ln{x})^3}{x} } \text{ } dx \]
Evaluate.
\[ \int_{\frac{\pi}{3}}^{\frac{2 \pi}{3}}{ \frac{ \cos{x}}{ \sqrt{\sin{x}}} } \text{ } dx \]
Evaluate.
\[ \int_{1}^{16}{ \frac{1}{\sqrt{x}(1+\sqrt{x})^2} } \text{ } dx \]
Evaluate.
\[ \int_{-2}^{1}{ x(x^2-3)^3 } \text{ } dx \]
Evaluate.
\[ \int_{\ln{2}}^{\ln{3}}{ e^{-2x} } \text{ } dx \]
Evaluate.
\[ \int_{0}^{\sqrt{3}}{ x \cdot e^{-x^2/3} } \text{ } dx \]
Evaluate.
\[ \int_{2}^{e+1}{ \frac{x}{(x-1)^2} } \text{ } dx \]
Using Polynomial Division Before Integrating
Integrate.
\[ \int{ \frac{x^3+2x^2-6}{x+2} } \text{ } dx \]
Evaluate.
\[ \int_{0}^{2}{ \frac{x^2-3}{x+2} } \text{ } dx \]
Integration by Parts
Theorems and Definitions
Integration by Parts
If \(u\) and \(v\) are functions of \(x\) and have continuous derivatives, then
\[ \int{ u } \text{ } dv = uv - \int{ v } \text{ } du. \]
Integrate by parts.
\[ \int{ \ln{x} } \text{ } dx \]
Integrate by parts.
\[ \int{ \sin{\sqrt{x}} } \text{ } dx \]
Integrate by parts.
\[ \int{ x \cdot \sin{x} } \text{ } dx \]
Integrate by parts.
\[ \int{ (\ln{x})^2 } \text{ } dx \]
Integrate by parts.
\[ \int{ \sin^{-1}{x} } \text{ } dx \]
Integrate.
\[ \int{ e^{\sqrt{x}} } \text{ } dx \]
Integrate.
\[ \int{ e^{\sqrt{-x}} } \text{ } dx \]
Integrate.
\[ \int{ x \sin^{-1}{x} } \text{ } dx \]
Finding the Area of a Bound Region
Find the area of the region bounded by the graphs of the equations.
\[ y=\frac{3}{4}x^2+x+1; \quad x=0; \quad y=0; \quad x=2 \]
The Mean Value Theorem for Integrals
Theorems and Definitions
The Mean Value Theorem for Integrals
If \(f\) is continuous on the closed interval \([a, b]\), then there exists a number \(c\) in the closed interval \([a, b]\) such that
\[ \int_{a}^{b}{ f(x) } \text{ } dx = f(c)(b-a). \]
Find the value(s) of \( c \) guaranteed by the Mean Value Theorem for Integrals.
\[ f(x)=\frac{1}{x} \quad [1, e^2] \]
Find the value(s) of \( c \) guaranteed by the Mean Value Theorem for Integrals.
\[ f(x)=\frac{1}{2x^2} \quad [1, 4] \]
Find the value(s) of \( c \) guaranteed by the Mean Value Theorem for Integrals.
\[ f(x)=6\sqrt{x} \quad [1, 4] \]
Find the value(s) of \( c \) guaranteed by the Mean Value Theorem for Integrals.
\[ f(x)=2\sec^2{x} \quad \Big[-\frac{\pi}{4}, \frac{\pi}{4} \Big] \]
contact@hsmathsolutions.com