Is the ordered pair \( P(-1, 5)\) a solution to the linear system?
\[ \left\{ \begin{array}{l} 3x+y=2 \\ -2x-3y=-8 \end{array}\right. \]
Is the ordered pair \( Q(3, -7)\) a solution to the linear system?
\[ \left\{ \begin{array}{l} 5x+4y=-13 \\ 2x-y=13 \end{array}\right. \]
Use the graph to classify the linear system.
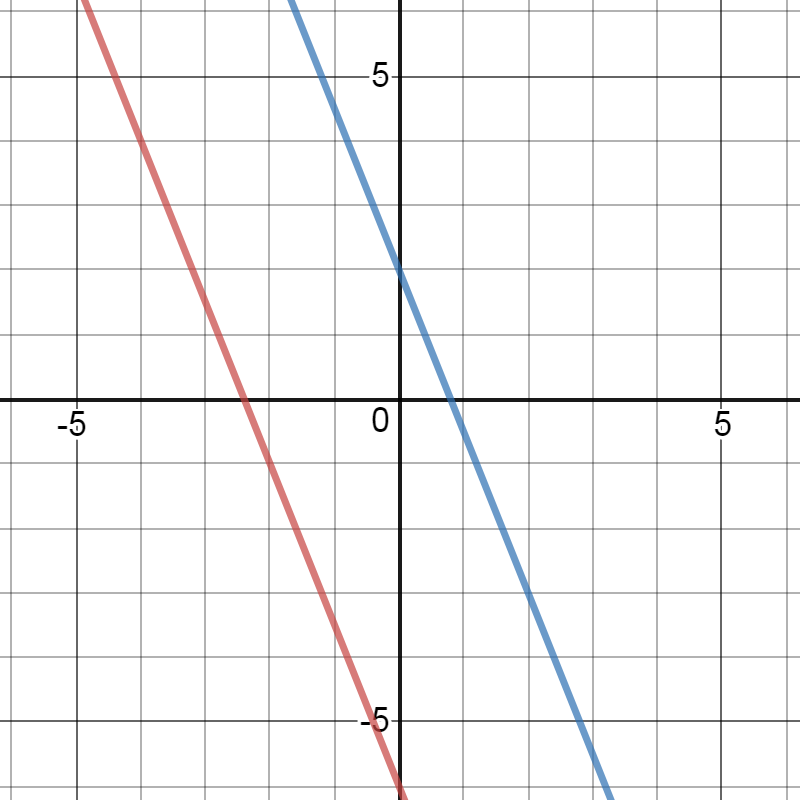
Use the graph to classify the linear system.
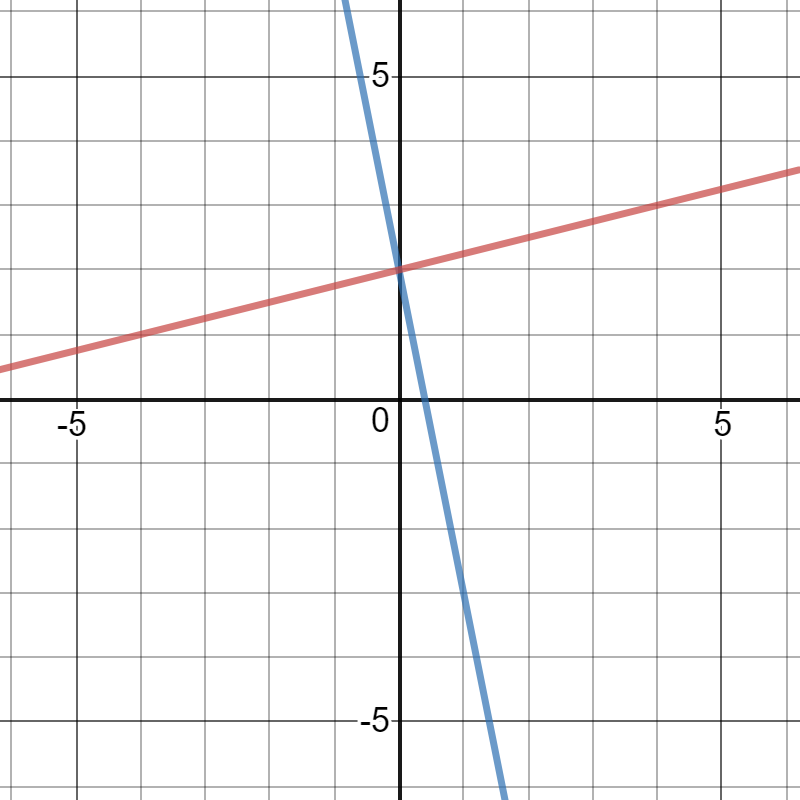
Use the graph to classify the linear system.
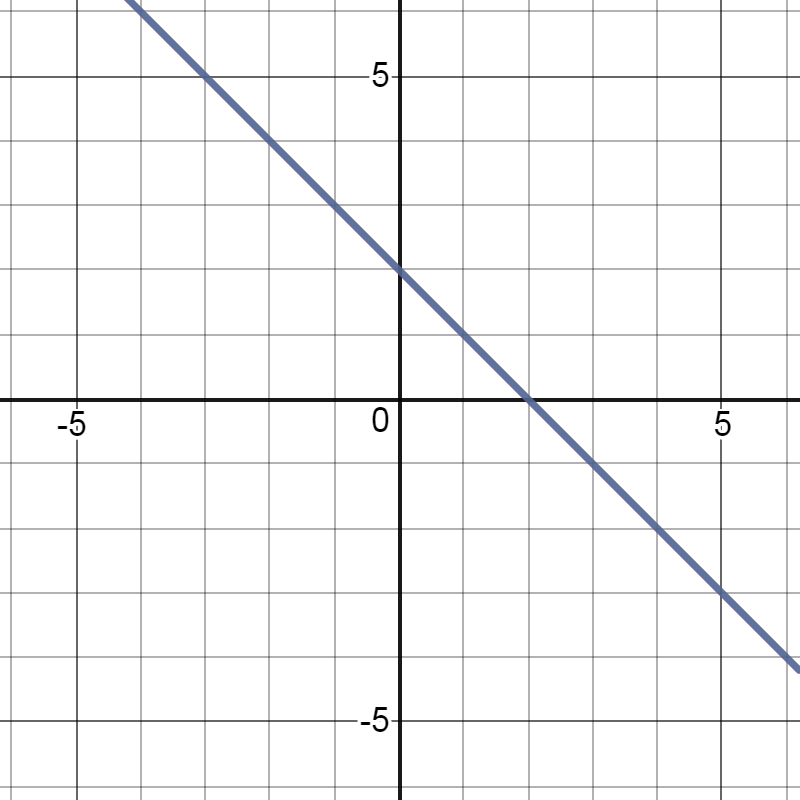
Determine the classification for the linear system.
\[ \left\{ \begin{array}{l} y=\frac{2}{3}x-5 \\ 3x-2y=8 \end{array}\right. \]
Determine the classification for the linear system.
\[ \left\{ \begin{array}{l} y-4=2(x+3) \\ -2x+y=5 \end{array}\right. \]
Determine the classification for the linear system.
\[ \left\{ \begin{array}{l} y=\frac{1}{3}x-2 \\ y+3=\frac{1}{3}(x+3) \end{array}\right. \]
Solve the system by graphing.
\[ \left\{ \begin{array}{l} y+4=\frac{1}{3}(x+6) \\ x-y=4 \end{array}\right. \]
Solve the system by graphing.
\[ \left\{ \begin{array}{l} 4x-3y=6 \\ y-2=\frac{4}{3}(x-3) \end{array}\right. \]
Solve the system by graphing.
\[ \left\{ \begin{array}{l} 2x-3y=-9 \\ y=5 \end{array}\right. \]
Solve the system by graphing.
\[ \left\{ \begin{array}{l} y=-3x-1 \\ 6x+2y=-8 \end{array}\right. \]
Solve the system by graphing.
\[ \left\{ \begin{array}{l} y-3=2(x+2) \\ y=-\frac{2}{5}x-5 \end{array}\right. \]
Determine values of \(a\) and \(b\) such that the linear system has a solution of \( P(4,-9) \).
\[ \left\{ \begin{array}{l} y=-\frac{1}{2}x+a \\ 2x+y=b \end{array}\right. \]
Determine values of \(a\) and \(b\) such that the linear system has infinite solutions.
\[ \left\{ \begin{array}{l} 2x-3y=a \\ y-1=b(x+6) \end{array}\right. \]
Evaluate the algebraic expression for the given values of the variable.
\[ \dfrac{6a^2}{b+1}+5ab \quad \quad a=-3 \text{, } b=2 \]
Evaluate the algebraic expression for the given values of the variable.
\[ \dfrac{m^2-5n}{3n+2m} \quad \quad m=-6 \text{, } n=3 \]
Evaluate the algebraic expression for the given values of the variable.
\[ -5a+2b \quad \quad a=x-1 \text{, } b=2x+9 \]
Evaluate the algebraic expression for the given values of the variable.
\[ 5y+2m-4n+5 \quad \quad m=-6y \text{, } n=3-5y \]
Solve by substitution.
\[ \left\{ \begin{array}{l} y=6x-20 \\ y=-2x+12 \end{array}\right. \]
Solve by substitution.
\[ \left\{ \begin{array}{l} 8x+8y=-24 \\ y=-2x-11 \end{array}\right. \]
Solve by substitution.
\[ \left\{ \begin{array}{l} -2x+5y=-17 \\ x-3y=9 \end{array}\right. \]
Solve by substitution.
\[ \left\{ \begin{array}{l} -x+7y=-9 \\ 3x-8y=1 \end{array}\right. \]
Solve by substitution.
\[ \left\{ \begin{array}{l} 2y-8x=5 \\ 4x-y=7 \end{array}\right. \]
Solve by substitution.
\[ \left\{ \begin{array}{l} y-2=3(x+1) \\ 3x-y=-5 \end{array}\right. \]
Solve by elimination.
\[ \left\{ \begin{array}{l} 3x-5y=20 \\ 2x+5y=5 \end{array}\right. \]
Solve by elimination.
\[ \left\{ \begin{array}{l} 5x+3y=-3 \\ -5x=4y-1 \end{array}\right. \]
Solve by elimination.
\[ \left\{ \begin{array}{l} 3x-3y=-12 \\ 2x=16-6y \end{array}\right. \]
Solve by elimination.
\[ \left\{ \begin{array}{l} -5x=20+5y \\ -10y=6x+28 \end{array}\right. \]
Solve by elimination.
\[ \left\{ \begin{array}{l} 2x+13=-7y \\ 9y-9=-9x \end{array}\right. \]
Solve by elimination.
\[ \left\{ \begin{array}{l} 3x=7y-23 \\ 2x-5y+16=0 \end{array}\right. \]
Solve by elimination.
\[ \left\{ \begin{array}{l} 18x-21y-10=0 \\ 6x=4+7y \end{array}\right. \]
Solve by elimination.
\[ \left\{ \begin{array}{l} 70y=7x-28 \\ -5x+20=-50y \end{array}\right. \]
Solve by elimination.
\[ \left\{ \begin{array}{l} \frac{3}{4}x+\frac{1}{2}y=3 \\ -\frac{1}{2}x-\frac{3}{2}y=5 \end{array}\right. \]
Determine values for \(a\) and \(b\) such that the solution to the linear system is \( Q(5, 3) \).
\[ \left\{ \begin{array}{l} ax-by=-2 \\ bx-ay=-14 \end{array}\right. \]
The sum of two numbers is 171. Also, the difference of twice the first number and the second number is 117.
Twice the first number, decreased by twenty-nine is three times the second number. Furthermore, three times the sum of the two numbers is 216.
Flying with the wind, an airplane travels at 620 miles per hour. However, traveling against the wind, the plane only travels at 570 miles per hour. Determine both the speed of the plane and the speed of the wind.
A boat traveling downstream travels at 23 kilometers per hour. However, the boat only travels 9 kilometers per hour upstream. Determine both the speed of the boat in still water and the speed of the current.
A local high school is selling tickets to the spring musical. On the first day, Julia sells 62 adult tickets and 27 student tickets for a total of $631. On the second day, she sells 48 adult tickets and 18 student tickets for a total of $474. Determine the price of both an adult ticket and a student ticket.
Olga and Maria are each improving their yards by planting geraniums and hibiscus plants. They purchased their supplies from the same store. Olga spent $225 on four geraniums and seven hibiscus plants. Maria spent $326 on six geraniums and ten hibiscus plants. Determine the cost of each plant.
Gerardo and Carlos are selling chocolate bars and cookies for a school fundraiser. Gerardo sold 48 chocolate bars and 120 cookies for a total of $192. Carlos sold 60 chocolate bars and 90 cookies for a total of $180. Determine the cost of both the chocolate bars and the cookies.
A boat traveled 72 miles each way downstream and back. The trip downstream took 4 hours. The trip back took 9 hours. What is the speed of the boat in still water? What is the speed of the current?
When you reverse the digits in a certain two-digit number you increase its value by 54. Find the number if the sum of its digits is 10.
Solve.
\[ \left\{ \begin{array}{l} -2a-2b-3c=20\\6a-6b+4c=-6\\-5a+4b+c=-19 \end{array}\right. \]
Solve.
\[ \left\{ \begin{array}{l} 2x+2y+3z=6\\-4x+4y-2z=4\\-2x+6y+z=10 \end{array}\right. \]
Solve.
\[ \left\{ \begin{array}{l} -2x-2y+4z=0 \\ 5x+2y+2z=-13 \\ x+2y-6z=-14 \end{array}\right. \]
Solve.
\[ \left\{ \begin{array}{l} -2x+3y+4z=1 \\ 5x-5y-4z=-20 \\ -3x-5y-6z=14 \end{array}\right. \]
Solve.
\[ \left\{ \begin{array}{l} 7a-2b+2c=-5 \\ -2a+5b-2c=-6 \\ -3a-8b+2c=17 \end{array}\right. \]
Solve.
\[ \left\{ \begin{array}{l} -6x-2y+2z=-8 \\ 3x-2y-4z=8 \\ 6x-2y-6z=-18 \end{array}\right. \]
Joan, Ana, and Natalie went shopping for Christmas decorations at the same store. Joan purchased four boxes of lights, seven ornaments, and two candles for $57. Ana purchased six boxes of lights, three ornaments, and one candle for $34. Natalie purchased 5 boxes of lights, four ornaments, and two candles for $44. Determine the unit cost of each item.
Solve.
\[ \left\{ \begin{array}{l} x-y=3 \\ y=x^2+3x-11 \end{array}\right. \]
Solve.
\[ \left\{ \begin{array}{l} xy=6 \\ 2x-y=4 \end{array}\right. \]
Solve.
\[ \left\{ \begin{array}{l} y=x^3-2 \\ y-2x^2+2=0 \end{array}\right. \]
Solve.
\[ \left\{ \begin{array}{l} x^2+y^2=4 \\ 2y=x^2-4 \end{array}\right. \]
Graph the system of linear inequalities.
\[ \left\{ \begin{array}{l} y \lt -x+3 \\ y \geq \frac{1}{3}x-3 \end{array}\right. \]
Graph the system of linear inequalities.
\[ \left\{ \begin{array}{l} y \geq -\frac{2}{3}x+2 \\ y \leq 2x-6 \end{array}\right. \]
Graph the system of linear inequalities.
\[ \left\{ \begin{array}{l} x+y \gt 5 \\ x-y \gt 1 \end{array}\right. \]
Graph the system of linear inequalities.
\[ \left\{ \begin{array}{l} 5x-3y \lt 6 \\ -2x+5y \lt -10 \end{array}\right. \]










