Algebra: Complex Numbers
Contents (14 topics • 81 videos)
Equality of Complex Numbers
Introduction Videos
Introduction to Complex Numbers 
Equality of Complex Numbers
Theorems and Definitions
Equality of Complex Numbers
Two complex numbers \( a+bi \) and \( c+di \), written in standard form, are equal to each other
\( a+bi = c+di \)
if and only if \( a=c \) and \( b=d \).
Find real numbers \(a\) and \(b\) such that the equation is true.
\[ a+bi = 8-3i \]
Find real numbers \(a\) and \(b\) such that the equation is true.
\[ (4a-1)-5bi=-9+15i \]
Find real numbers \(a\) and \(b\) such that the equation is true.
\[ -11+(6b)i=(3a-2)-i \sqrt{6} \]
Determine the complex number \( a+bi \) represented by the system.
\[ \left\{ \begin{array}{l} 2a+b=-1 \\ 4b=1-7a \end{array}\right. \]
Documents
Practice Problems (.PDF) 
Practice Problems - Solutions (.PDF) 
Writing Complex Numbers in Standard Form
Introduction Videos
Simplifying Higher Powers of \( i \)
Simplifying Positive and Negative Square Roots
Theorems and Definitions
Imaginary Numbers
An imaginary number is the square root of a negative number.
\( \sqrt{-25} \)
Imaginary numbers can be written in the form \(bi\), where \(b\) is a real number and \(i\) is the imaginary unit, \(\sqrt{-1}\).
\( \sqrt{-25} = \sqrt{25} \times \sqrt{-1} = 5i \)
The square of an imaginary number is the original negative number.
\( (5i)^2 = 25i^2 = 25(-1) = -25 \)
Simplify.
\[ i^{37}+3i^{25} \]
Simplify.
\[ 11i^{10}-6i^{28} \]
Write the complex number in standard form.
\[ 5+\sqrt{-49} \]
Write the complex number in standard form.
\[ \frac{\sqrt{-81}}{6} \]
Write the complex number in standard form.
\[ -\sqrt{108}+\sqrt{-50} \]
Write the complex number in standard form.
\[ \Big( \sqrt{-18} \Big)^3 \]
Write the complex number in standard form.
\[ (2i^3)^5 \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
Adding and Subtracting Complex Numbers
Introduction Videos
Adding and Subtracting Complex Numbers
A Visualization of Addition and Subtraction with Complex Numbers
Theorems and Definitions
Addition and Subtraction of Complex Numbers
If \( a+bi \) and \( c+di \) are two complex numbers written in standard form, then their sum and difference are defined as follows.
Sum: \( (a+bi)+(c+di) = (a+c)+(b+d)i \)
Difference: \( (a+bi)-(c+di) = (a-c)+(b-d)i \)
The Additive Inverse of a Complex Number
The additive identity in the complex number system is zero (as in the real number system). The additive inverse of any complex number \(a+bi\) is
\( -(a+bi) = -a-bi \)
It follows from the previous definition of addition of complex numbers that
\( (a+bi) + (-a-bi) = 0+0i = 0 \)
Simplify. Write the result in standard form.
\[ (9-2i)+(-3-5i)-(6-i) \]
Simplify. Write the result in standard form.
\[ (-3+\sqrt{-12})+(9+\sqrt{-27}) \]
Simplify. Write the result in standard form.
\[ \Bigg( -\frac{11}{6}+\sqrt{-\frac{45}{4}} \Bigg)- \Bigg(\frac{2}{3}-\sqrt{-\frac{20}{9}} \Bigg) \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
Multiplying Complex Numbers
Introduction Videos
Multiplying Complex Numbers
Higher Powers of Complex Numbers
A Visualization of Multiplying by \(i\)
Theorems and Definitions
Multiplication of Complex Numbers
If \( a+bi \) and \( c+di \) are two complex numbers written in standard form, then using the distributive property, their product can be shown as follows.
\( \quad (a+bi)(c+di) \\ = ac+(ad)i+(bc)i+(bd)i^2 \\ = ac+(ad+bc)i+(bd)(-1) \\ = (ac-bd)+(ad+bc)i \)
Simplify. Write the result in standard form.
\[ 2i \cdot -5i \cdot 3i \]
Simplify. Write the result in standard form.
\[ 4i(2-3i) \]
Simplify. Write the result in standard form.
\[ (-3+7i)(5-2i) \]
Simplify. Write the result in standard form.
\[ (3-i)(3+i)(3+i) \]
Simplify. Write the result in standard form.
\[ (\sqrt{7}-\sqrt{10}i)(\sqrt{7}+\sqrt{10}i) \]
Simplify. Write the result in standard form.
\[ (2+3i)^2 \]
Simplify. Write the result in standard form.
\[ (-6+i)^3 \]
Cube the complex number. Write the result in standard form.
\[ -1-\sqrt{3}i \]
Cube the complex number. Write the result in standard form.
\[ \frac{3}{2}+\frac{3\sqrt{3}}{2}i \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
Writing Complex Conjugates
Introduction Videos
Complex Conjugates
Theorems and Definitions
Complex Conjugates
If \( a+bi \) is a complex number, then its complex conjugate is \(a-bi\); their real parts are equal but their imaginary parts are opposites.
The product of multiplying a complex number with its complex conjugate always results in a real number (the \(i\) will always cancel).
\( \quad (a+bi)(a-bi) \\ = a^2-(ab)i+(ab)i-b^2i^2 \\ =a^2-b^2(-1) \\ =a^2+b^2 \)
Multiply the complex number by its complex conjugate.
\[ -4+3i \]
Multiply the complex number by its complex conjugate.
\[ -7i \]
Multiply the complex number by its complex conjugate.
\[ -3-\sqrt{2}i \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
Dividing Complex Numbers
Introduction Videos
Division by an Imaginary Number
Dividing Complex Numbers
Theorems and Definitions
Division of Complex Numbers
If \( a+bi \) and \( c+di \) are complex numbers, their quotient is found by rationalizing the denominator, that is, multiplying both the numerator and denominator by the complex conjugate of the denominator.
\( \quad \frac{a+bi}{c+di} \\ = \frac{a+bi}{c+di} \cdot \frac{c-di}{c-di} \\ = \frac{(a+bi)(c-di)}{c^2+d^2}\)
By multiplying the denominator by its complex conjugate, the product is always a real number.
Write the quotient in standard form.
\[ \frac{3}{2i} \]
Write the quotient in standard form.
\[ \frac{5-i}{-4i} \]
Write the quotient in standard form.
\[ \frac{2i}{3-6i} \]
Write the quotient in standard form.
\[ \frac{5-2i}{-6+i} \]
Write the quotient in standard form.
\[ \frac{2-i}{2+i} \]
Write the quotient in standard form.
\[ \frac{-6+i}{(1-3i)^2} \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
More Operations with Complex Numbers
Introduction Videos
More Operations with Complex Numbers
Simplify. Write the result in standard form.
\[ \frac{5}{3-i}+\frac{2}{3+i} \]
Simplify. Write the result in standard form.
\[ \frac{4i}{4+i}-\frac{4+3i}{11-7i} \]
Determine values of \(a\) and \(b\) that satisfy the equation.
\[ \frac{a}{3+2i}+\frac{bi}{3-2i}=4-i \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
Graphing Complex Numbers in the Complex Plane
Use the graph to write each complex number.
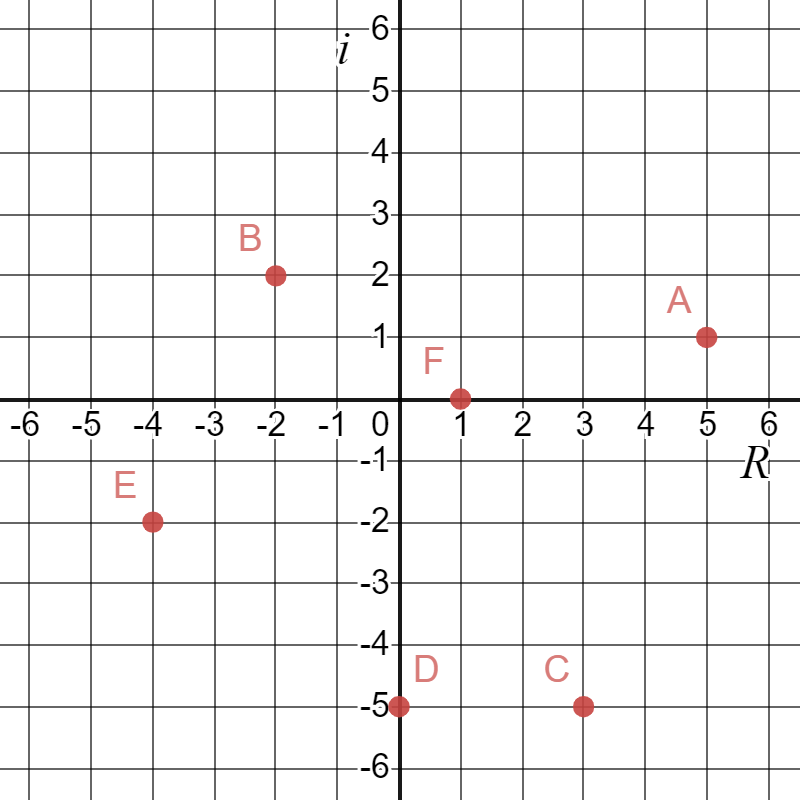
Plot each complex number on the complex plane.
\( \text{A} \quad -2+6i \\ \text{B} \quad 4 \\ \text{C} \quad 5-i \\ \text{D} \quad 3+3i \\ \text{E} \quad -2i \\ \text{F} \quad -1-4i \)
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
Graph Paper (.PDF) 
Calculations in the Complex Plane
Introduction Videos
The Absolute Value of a Complex Number
The Distance Between Two Complex Numbers in the Complex Plane
The Midpoint of Two Complex Numbers in the Complex Plane
A Visualization of Addition and Subtraction with Complex Numbers
Theorems and Definitions
The Absolute Value of a Complex Number
The absolute value, also called the modulus, of the complex number \( z=a+bi \) is
\( \big| a+bi \big| = \sqrt{a^2+b^2} \).
The Distance Between Two Complex Numbers
The distance between two complex numbers, \( z_1 = a+bi \) and \( z_2 = c+di \), in the complex plane is
\( d = \sqrt{(c-a)^2+(d-b)^2} \).
This quantity is equal to the modulus of the difference of the two complex numbers.
\( d = \big| z_2-z_1 \big| = \big| (c-a)-(d-b)i \big| \)
The Midpoint of Two Complex Numbers
The midpoint of two complex numbers, \( z_1 = a+bi \) and \( z_2 = c+di \), in the complex plane is
\( \frac{a+c}{2} + \frac{b+d}{2}i \).
This quantity is equal to the average of the two complex numbers that make up the endpoints of the line segment.
\( \frac{z_1+z_2}{2}\)
Calculate the absolute value.
\[ \big| 3-4i \big| \]
Calculate the absolute value.
\[ \big| 5\sqrt{2}+6i \big| \]
Calculate the distance between the two complex numbers.
\[ 2+7i \quad \quad 5+3i \]
Calculate the distance between the two complex numbers.
\[ -5i \quad \quad -4+3i \]
Calculate the midpoint of the line segment for which the pair of complex numbers are endpoints.
\[ 3+7i \quad \quad -1+21i \]
Calculate the midpoint of the line segment for which the pair of complex numbers are endpoints.
\[ -3\sqrt{2}+\sqrt{11}i \quad \quad \sqrt{2}+6\sqrt{11}i \]
Determine the midpoint of the line segment whose endpoints are the given point and its complex conjugate.
\[ 7-2i \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
Graph Paper (.PDF)
Factoring Binomials with Complex Factors
Introduction Videos
Sum and Difference of Squares Factorizations
Theorems and Definitions
Difference and Sum of Squares Factorizations
The difference of squares factorization is given by
\( a^2-b^2=(a+b)(a-b) \).
The sum of squares factorization is given by
\( a^2+b^2=(a+bi)(a-bi) \).
Factor.
\[ x^2+16 \]
Factor.
\[ 5p^2-45 \]
Factor.
\[ j^4-81 \]
Use the sum/difference of squares formulas to multiply.
\[ (3n-11i)(3n+11i) \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
Solving Equations with Complex Roots
Introduction Videos
Solving Equations by Factoring (Complex Roots)
Theorems and Definitions
The Quadratic Formula
For a quadratic equation of the form \( ax^2+bx+c=0 \), where \(a\), \(b\), and \(c\) are real number constants and \( a \ne 0 \),
\[ x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} \]
Solve by factoring.
\[ x^2+36=0 \]
Solve by factoring.
\[ 3x^3=-135x \]
Solve by factoring.
\[ 363x^2+3=0 \]
Solve using the quadratic formula.
\[ x^2-4x+13=0 \]
Solve using the quadratic formula.
\[ x^2+2\sqrt{2}x+7=0 \]
Solve using the quadratic formula.
\[ x^2-(2a)x+(a^2+b^2)=0 \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
Multiplying Expressions with Complex Numbers
Introduction Videos
Multiplying Expressions that Contain Complex Conjugates
Multiply.
\[ (2x-3\sqrt{5}i)(2x+3\sqrt{5}i) \]
Multiply.
\[ (x+1-8i)(x+1+8i) \]
Multiply.
\[ \Big( x-1-\sqrt{5}+\sqrt{3} i \Big) \Big( x-1+\sqrt{5}-\sqrt{3} i \Big) \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
Writing Quadratic Functions from Complex Roots
Introduction Videos
Writing Quadratic Functions from Complex Roots
Theorems and Definitions
Writing Quadratic Functions from Complex Roots
If a quadratic function has complex roots
\[ x=a+bi, a-bi \]
then the quadratic function can be written in the form
\[ f(x)=(x-(a+bi))(x-(a-bi)) \]
\[ f(x)=(x-a-bi)(x-a+bi) \]
\[ f(x)=x^2-2ax+a^2+b^2 \]
Write a quadratic function for the set of complex roots.
\[ x= \pm 3i \]
Write a quadratic function for the set of complex roots.
\[ x=5+\sqrt{2}i, 5-\sqrt{2}i \]
Write a quadratic function for the set of complex roots.
\[ x=-4+\frac{2\sqrt{6}}{3}i, -4-\frac{2\sqrt{6}}{3}i \]
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
A Check for Conceptual Understanding
Documents
Practice Problems (.PDF)
Practice Problems - Solutions (.PDF)
contact@hsmathsolutions.com